DASCTF2023年7月赛

July 31, 2023

controlflow #

这个程序的控制流好像有点奇怪

可以通过识别 push ebp 来确定真实的函数的位置

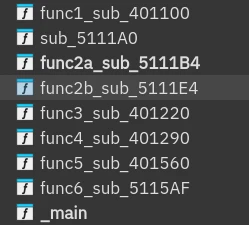
设置函数起始处跳过这些插入的代码块并勾选 BP-Based Frame 可以成功 F5

每个小函数上下断点可以找到执行的顺序如下

main -> func3 -> func5 -> func6 -> func2b -> func1 -> func4

main 函数中最后一段还有一部分加密代码

main: a[i]^=0x401
func3: a[i]+=i**2
func5: a[j]^=j*(j+1) for j in range(10,30)
func6: a[i]-=i
func2b: a[i]*=3
func4: swap(a[k+1],a[k]) for k in range(10,30,2)

解密并不难

s = [
    3279, 3264, 3324, 3288, 3363, 3345, 3528, 3453, 3498, 3627, 3708,
    3675, 3753, 3786, 3930, 3930, 4017, 4173, 4245, 4476, 4989, 4851,
    5166, 5148, 4659, 4743, 4596, 5976, 5217, 4650, 6018, 6135, 6417,
    6477, 6672, 6891, 7056, 7398, 7650, 7890
]

# func4
for i in range(10, 30, 2):
    s[i + 1], s[i] = s[i], s[i + 1]

# func2b
for i in range(40):
    assert s[i] % 3 == 0
    s[i] //= 3

# func6
for i in range(40):
    s[i] += i

# func5
for i in range(20):
    s[10 + i] ^= i * (i + 1)

# func3
for i in range(40):
    s[i] -= i * i

# main
for i in range(40):
    s[i] ^= 0x401

flag = "".join(chr(b) for b in s)
print(flag)
#DASCTF{TWpnemRuSTRkVzVsWVhOMmJqZzNOREoy}

感觉这题其实是可以 angr 一把梭的，没试

几个花指令的形式可以参考一下，以后可能有用

webserver #

基于 OATPP 的 webserver

每个 Handler 都是一个 C++ 类，先找 Handler 的虚表

可以通过类名字定位

交叉引用第一次是 typeinfo

交叉引用第二次就是 vtable 了

检查函数位于 CheckHandler.sub_40617E

开头这一段是通过反转比特解密字符串，用于对抗字符串搜索，简单修补了一下

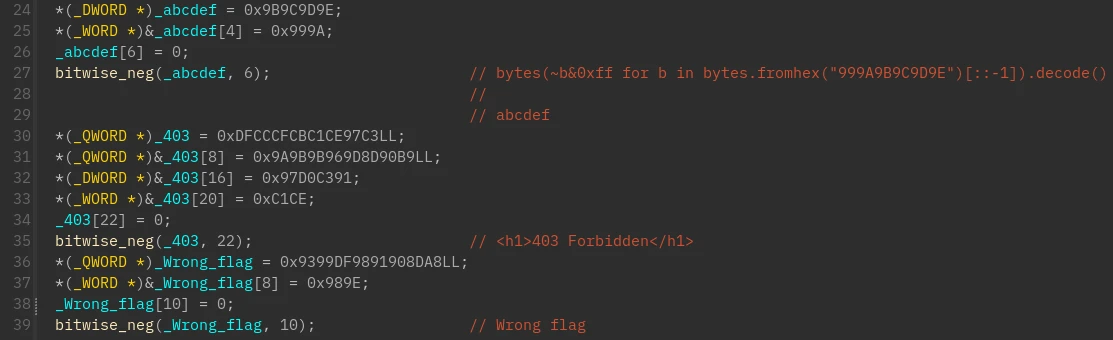
第 52 行后也修补了一下（加了一个 string 的类型），是在将 string 转化成 4x10 的 int 矩阵

第 101 行之后就是在做矩阵相乘

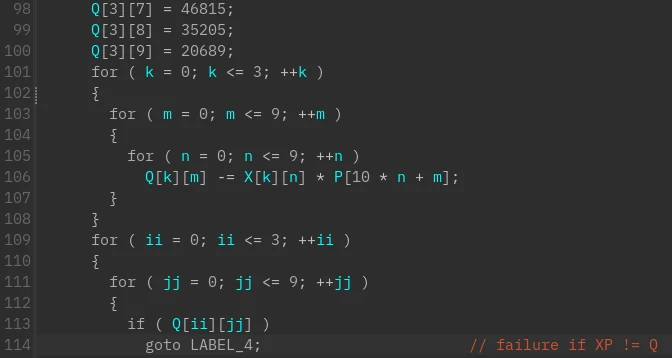
综合以上可以猜测，需要向 webserver 发送一个 GET 请求 abcdef=${flag}

flag 内容是解矩阵方程 $\mathbf{X}\times \mathbf{Q}=\mathbf{P}$ 的结果，其中 $\mathbf{Q}$ 和 $\mathbf{P}$ 都是已知的

from sympy import Matrix

P = Matrix(
    [
        [33211, 36113, 28786, 44634, 30174, 39163, 34923, 44333, 33574, 23555],
        [35015, 42724, 34160, 49166, 35770, 45984, 39754, 51672, 38323, 27511],
        [31334, 34214, 28014, 41090, 29258, 37905, 33777, 39812, 29442, 22225],
        [30853, 35330, 30393, 41247, 30439, 39434, 31587, 46815, 35205, 20689],
    ]
)

Q = Matrix(
    [
        [23, 13, 4, 48, 41, 41, 42, 33, 30, 3],
        [69, 1, 13, 45, 41, 64, 8, 80, 15, 42],
        [56, 19, 62, 70, 23, 63, 30, 68, 17, 56],
        [92, 12, 16, 64, 31, 3, 17, 71, 58, 9],
        [64, 83, 71, 52, 99, 89, 76, 68, 1, 99],
        [16, 16, 52, 43, 0, 44, 50, 32, 50, 31],
        [20, 63, 2, 99, 0, 57, 79, 43, 71, 19],
        [80, 92, 93, 58, 84, 74, 81, 45, 55, 21],
        [1, 99, 30, 28, 56, 1, 12, 77, 92, 4],
        [37, 67, 60, 54, 51, 79, 38, 87, 48, 16],
    ]
)

invQ = Q.inv_mod(256)
X = P * invQ
flag = ""
for i in range(4):
    for j in range(10):
        flag += chr(X[i, j] & 0xFF)

print(flag)
#DASCTF{CI5ZCM5piv5aaC5L2V5pS26LS555qE5Y}

TCP #

小王是你的好朋友
最近他们公司下发了一个程序进行逆向竞赛
此程序会和公司内网的某个服务器建立TCP连接
小王需要你帮他找到PASSWORD
此外，小王已经发现，PASSWORD并不在服务器进行判断
由于你无法访问公司内网，小王贴心地给你抓了网络包(1.pcapng)并把程序给你(c)

main 函数首先从服务器接收一个 32 只的串

传入一个以该串和不知名全局变量 unk_5060 为参数的函数 sub_2090

然后把长度为 96 的输出再送回服务器，这是在和服务器密钥交换

sub_2090 -> sub_1f9c -> sub_1e6e

sub_1e6e 是 128 位带模乘法

修复这个函数需要设置变量类型和返回类型为 __int128

除此之外，由于传递参数时使用了大量寄存器（一个 __int128 就要用两个寄存器），函数会将参数缓存到栈上以腾出寄存器空间

F5 里可以看到许多临时变量，需要将它们绑定到参数上

sub_1f9c 有和它类似的结构，为 128 位快速幂

再往前推断可知，sub_2090 就是块大小为 8 的 RSA 分块加密

密钥是 32 位字串，前 16 位是 n，后 16 位是 e

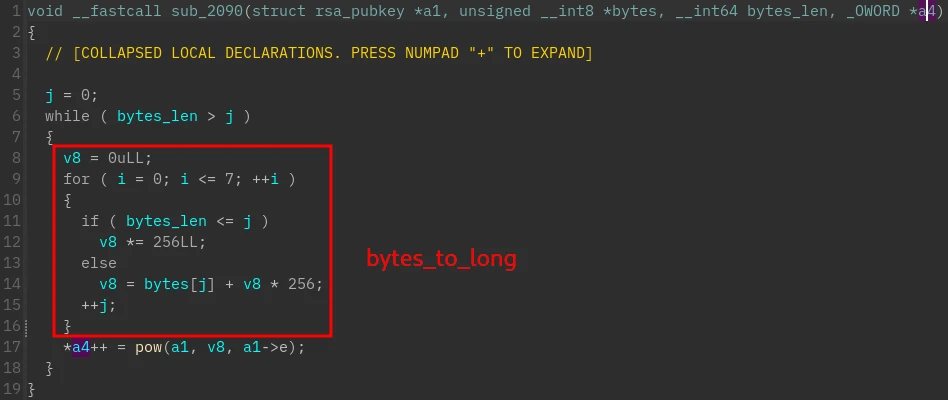
然而 128 位的 n 并不大，直接放到 factordb 解密

$p=1152921504606848051, q=2152921504606847269$

至于参数 bytes 可以对调用时的参数 unk_5060 交叉引用，发现这是一个初始化为随机值的字串，长度 48

总结密钥交换：

服务器生成 128 位的 n 和 e 发送给客户端
客户端生成 48 字节的数据（暂时未知加密算法）用 e 加密送给服务器

继续看 main 函数，密钥交换过后它从服务器再拿 12 字节并通过 sub_1d9a

显然这是在解密服务器的数据，不然也就不用交换密钥了

逻辑很简单，其中 sub_1c0a 是块长度 64 的 TEA 解密

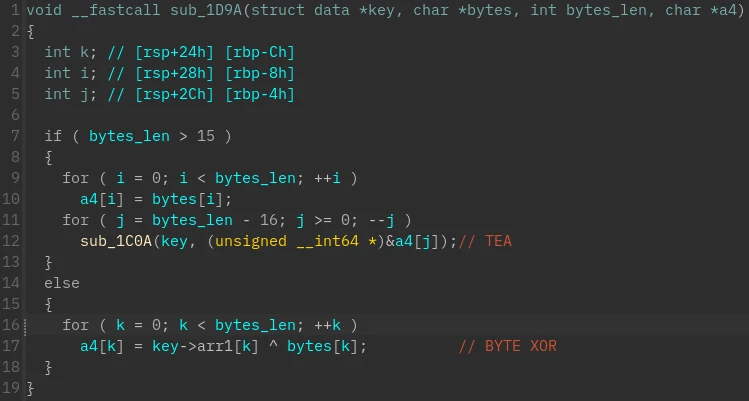
XOR 的密钥为 48 字节数据的后 16 字节，TEA 的 4 个密钥为前 32 字节

继续分析接收的 12 字节数据，main 函数将其分为 3 个整数，第一个整数为 RPC 调用号，后两个整数为参数，功能如下：

接收 c 字节，解密后打印
接收 c 字节，解密后存到“内存”里，段号为 b
读取输入，将每个字符转成 __uint32 存到“内存”里，段号为 b
打印 b 段处的字符
执行 b 段处的指令
退出

其中每段长度为 400

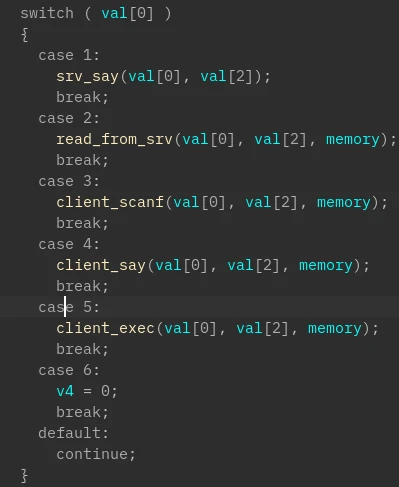
因此我们只需要模拟客户端的动作把“内存”转储下来分析即可

def tea_decrypt(d):
    v0 = u64(d[0:8])
    v1 = u64(d[8:16])
    s = 0x13c6ef3720
    MASK = 2**64-1
    for i in range(32):
        tmp = ((v0 + s) ^ ((v0 << 4) + tea_key[2]) ^ ((v0 >> 5) + tea_key[3])) & MASK
        v1 = (v1 - tmp) & MASK
        tmp = ((v1 + s) ^ ((v1 << 4) + tea_key[0]) ^ ((v1 >> 5) + tea_key[1])) & MASK
        v0 = (v0 - tmp) & MASK
        s = (s - 0x9e3779b9) & MASK
    return p64(v0) + p64(v1)

def decrypt(m):
    l = len(m)
    if l > 15:
        b = bytearray(m)
        for i in range(l-16, -1, -1):
            b[i:i+16] = tea_decrypt(b[i:i+16])
        return bytes(b)
    else:
        return bytes(m[i] ^ xor_key[i] for i in range(len(m)))

buf = bytearray(400 * 10)
i = 0

while True:
    insn = decrypt(msg[i:i+12])
    i += 12
    a0,a1,a2 = u32(insn[0:4]),u32(insn[4:8]),u32(insn[8:12])
    if a0 == 1:
        print(f'SRV  says: {decrypt(msg[i:i+a2]).decode()}')
        i += a2
    elif a0 == 2:
        data = decrypt(msg[i:i+a2])
        i += a2
        buf[400*a1:400*a1+a2] = data
        print(f'CLNT does: read from SRV to segment {a1}')
    elif a0 == 3:
        print(f'CLNT does: read from stdin to segment {a1}')
    elif a0 == 4:
        print(f'CLNT does: print segment {a1}')
    elif a0 == 5:
        print(f'CLNT does: exec code at segment {a1 & 0xffff}')
    else:
        print('CLNT quit')
        break

with open('program', 'wb') as f:
	f.write(buf)

SRV  says: Hello, this is the remote server.

CLNT does: read from SRV to segment 1
CLNT does: read from SRV to segment 2
SRV  says: Please enter your password

CLNT does: read from stdin to segment 0
CLNT does: read from SRV to segment 8
CLNT does: read from SRV to segment 4
CLNT does: read from SRV to segment 5
CLNT does: read from SRV to segment 6
CLNT does: read from SRV to segment 7
CLNT does: exec code at segment 8
CLNT does: print segment 3
CLNT quit

分析转储的 program，非常平凡的实现

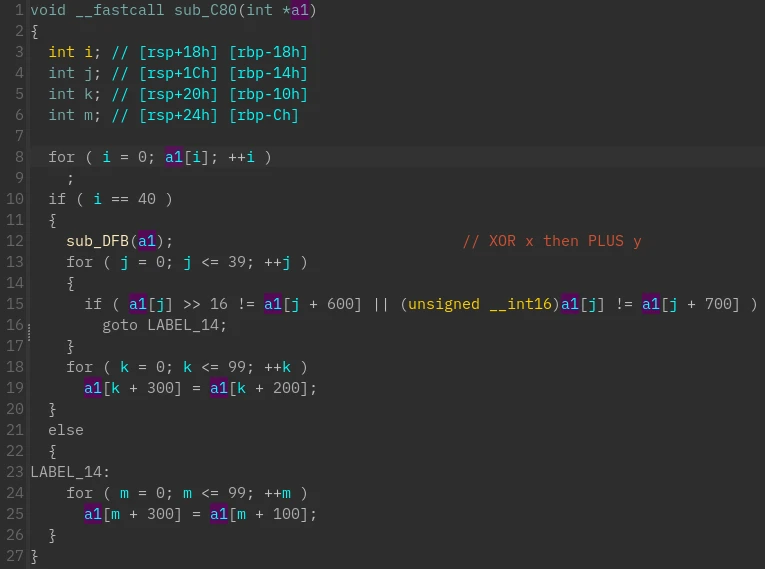
DASCTF{5rOV562J5Y5pu+5amn6Zuv2B5aSa5Liq}

ezDHKE #

DHKE is easy, huh?

Diffie Hellman，但模数任选

如果选取 $p$ 使得 $g^k = p+1$，当 $t < k$, $g^t < p$

有 $C_x = g^x \pmod{p} = g^{x \bmod{k}} \pmod{p} = g^{x \bmod{k}}$

我们直接在 $\mathbb{Z}$ 上求 $\log_g{C_x}$ 即得到 $x \bmod{k}$

对 $y$ 同理然后可以得到

$K$ = $g^{xy}\pmod{p}=g^{xy \bmod k} \pmod{p}=g^{(x\bmod k)(y \bmod k)} \pmod{p}$

本题中 $g=2$，这更容易了

DASCTF{eefa6be7-57e6-4a48-99d6-936feff93108}

ezRSA #

RSA is not easy, huh?

这是两道 RSA 的缝合题

第一关：知道 $P \otimes (Q»16)$ 要分解 $N$，这一步结束可以得到第二步的 $n$

第二关：知道前后缀、密文以及带前后缀的密文求明文

从第 0 位一直到第 495 位每一位的组合只有两种情况，并且满足

$\bar{P} * \bar{Q} \pmod{2^l} \equiv P * Q \pmod{2^l} = N \pmod{2^l}$

其中 $l$ 是位数

直接进行深度优先搜索即可

$Q$ 的低 16 位完全未知只能纯粹枚举

注意这里有一点比较坑，$n$ 求解之后长度只有 1020 完全不够

需要加上 $N$ (如果加上 $2N$ 长度就超过了)

然后是一个 related message attack

可以考虑 coppersmith

不过更方便的办法是用 gcd

dasctf{C0pper_Sm1th_Mak3s_T1ng5_Bet4er}

ezAlgebra #

Algebra is not easy!

取 3 个质数 $p \in {{0,1}}^{512}, q \in {{0,1}}^{256}, r \in {{0,1}}^{256}$

告知 $n=pqr$

选取 $t \overset{\$}{\leftarrow} {\set{0,1}}^{32}$

输出

$c_1 = 1997 + (p+t) + (p+t)^2 + (p+t)^3 + (p+t)^4 \pmod{n}$

$c_2 = 1997 + \sum_{i=0}^{19} m^it^i \pmod{q}$

$c_3 = 1997 + \sum_{i=0}^{19}(m+t)^i \pmod{q}$

其中 $m$ 就是 flag

注意到 $c_1 \equiv 1997 + t + t^2 + t^3 + t^4 \equiv 0 \pmod{p}$

回顾一下 coppersmith 的约束

$$ \begin{align*} X &\sim N^{\frac{\beta^2}{\delta}-\epsilon} \newline p^\beta &= N \newline \delta &= \deg{f} \newline \end{align*} $$

简单估算一下参数

$$ \begin{align*} \delta &= 4 \newline \beta &\sim \frac{1}{2} \newline \frac{\beta^2}{\delta}-\epsilon&>\frac{32}{1024}=\frac{1}{32} \newline \end{align*} $$

取 $\epsilon$ 为 $\frac{1}{33}$ 即可

得到 $t$ 后计算 $p = \gcd(c_1,n)$ 得到 $N = qr = \frac{n}{p}$

接下来还需要分解 $N$，在 $\mathbb{Z}[x]/N$ 上定义

$f(x) = 1997 + \sum_{i=0}^{19} x^it^i - c_2$

$g(x)= 1997 + \sum_{i=0}^{19}(x+t)^i - c_3$

由于 $q|f(m)$, $q|g(m)$ 有

$q_0=\gcd(f,g) \in \mathbb{Z}_N$ 且 $q|q_0$

计算 $q=\gcd(q_0,N)$ 即可

在 $\mathbb{Z}[x]/q$ 上定义

$\bar{f}(x) = f(x) \pmod{q}$

$\bar{g}(x) = g(x) \pmod{q}$

一定有 $(x-m)^{\alpha} = \gcd(\bar{f}, \bar{g})$

令 $x=m+kq$ 爆破明文

dasctf{ShangPoXiaPoYaSiLeYiQianDuo}

还在玩梗 -_-