GDGAlgiersCTF2022
Traditions #
假随机,种子 0x7E6
import ctypes
libc = ctypes.CDLL("libc.so.6")
libc.srand(0x7E6)
stream = [libc.rand() for i in range(47)]
Oldschool #
You'll probably recognize this format just by looking at the size of the binary file.
512 字节的 MBR 块
BIOS 会将 MBR 装载到 0x10000 的地址空间中,起始地址为 0x7C00
MBR 部分以程序指针被置零结束
这里使用 unicorn 加载并调试
from unicorn import *
from unicorn.x86_const import *
from capstone import *
base_addr = 0x7C00
entry_point = base_addr
mem_size = 0x10000
with open("oldschool", "rb") as fp:
mbr = fp.read()
def emu(flag):
mu = Uc(UC_ARCH_X86, UC_MODE_16)
md = Cs(CS_ARCH_X86, CS_MODE_16)
mu.mem_map(0, mem_size)
mu.mem_write(base_addr, mbr[:512])
mu_stdin = flag
mu_stdout = []
def hook_code(mu, address, size, user_data):
nonlocal md
code = mu.mem_read(address, size)
insns = list(md.disasm(bytes(code), address, count=1))
if len(insns) == 0:
raise Exception(f"cant disasm insn at {address}")
insn = insns[0]
address = insn.address
size = insn.size
mnemonic = insn.mnemonic
op_str = insn.op_str
print("%.8x:\t%s\t%s" % (address, mnemonic, op_str))
if address == 0x7c6a:
ax = mu.reg_read(UC_X86_REG_AX)
bx = mu.reg_read(UC_X86_REG_BX)
dx = mu.reg_read(UC_X86_REG_DX)
di = mu.reg_read(UC_X86_REG_DI)
print("ax: %.4x\tbx: %.4x\tdx: %.4x\tdi: %.4x" % (ax, bx, dx, di))
def hook_intr(mu, intno, user_data):
nonlocal mu_stdin
nonlocal mu_stdout
ah = mu.reg_read(UC_X86_REG_AH)
al = mu.reg_read(UC_X86_REG_AL)
di = mu.reg_read(UC_X86_REG_DI)
if intno == 0x10:
if ah == 0x0E: # print char
mu_stdout.append(al)
elif intno == 0x16:
mu.reg_write(UC_X86_REG_AL, mu_stdin[di - 0x7D80])
else:
raise Exception("unk intr no: %xh" % intno)
try:
mu.hook_add(UC_HOOK_CODE, hook_code)
mu.hook_add(UC_HOOK_INTR, hook_intr)
mu.emu_start(begin=entry_point, until=0)
except Exception as e:
print(e)
mu.emu_stop()
return bytes(mu_stdout)
out=emu(b"0123456789ABCDEF")
print(bytes(out).decode())
上述模板将打印程序执行流,部分执行流如下
00007c5e: rol ax, 8
00007c61: rol bx, 8
00007c64: rol dx, 8
00007c67: rol di, 8
00007c6a: push ax
ax: 3233 bx: 3031 dx: 3435 di: 3637
00007c6b: and ax, 0xf0f
00007c6e: cmp ax, 0xd02
00007c71: je 0x7cbf
00007c73: cmp ax, 0x700
00007c76: je 0x7c8c
00007c78: mov ax, word ptr ss:[esp]
00007c7d: and ax, 0xff
00007c80: cmp ax, 0x54
00007c83: je 0x7ca4
00007c85: and ax, 0xf
00007c88: cmp al, 2
00007c8a: je 0x7cd0
00007c8c: xor bx, dx
00007c8e: xor bh, 0xf
00007c91: and bx, 0xff00
00007c95: and di, 0xff00
00007c99: cmp bx, di
00007c9b: jne 0x7ce5
00007ce5: mov word ptr [0x7d88], 0
00007ceb: pop ax
00007cec: inc cx
00007ced: jmp 0x7c29
总共输入 8 个字符,做 4 次检查,每次检查的输入为不同的排列
可以观察到 0x7c5e 处是派发函数
0x7ce5 将结果置为假
4 次输入不同的排列可以用 unicorn 调试得出
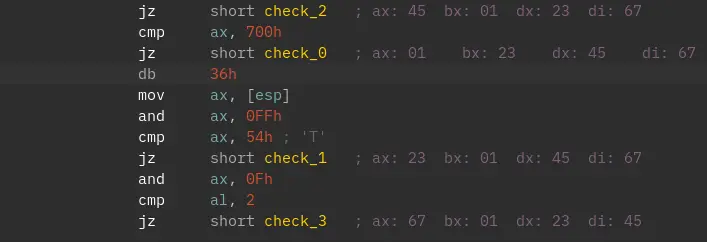
使用 z3 约束求解即可
import z3
from Crypto.Util.number import long_to_bytes as l2b
S = z3.Solver()
flags = [z3.BitVec("s%d" % i, 16) for i in range(4)]
flag = z3.Concat(*flags)
# check 0
ax, bx, dx, di = flags[0], flags[1], flags[2], flags[3]
S.add(ax & 0x0F0F == 0x700)
bx ^= dx
bx ^= 0x0F00
bx &= 0xFF00
di &= 0xFF00
S.add(bx == di)
# check 1
ax, bx, dx, di = flags[1], flags[0], flags[2], flags[3]
S.add(ax & 0xFF == 0x54)
bx ^= dx
bx = z3.RotateLeft(bx, 1)
bx ^= 0xF0
bx &= 0xF0F0
di &= 0xF0F0
S.add(bx == di)
# check 2
ax, bx, dx, di = flags[2], flags[0], flags[1], flags[3]
S.add(ax & 0x0F0F == 0x0D02)
bx ^= dx
bx ^= 0x3536
S.add(bx == di)
# check 3
ax, bx, dx, di = flags[3], flags[0], flags[1], flags[2]
S.add(ax & 0x0F == 2)
bx ^= dx
bx &= 0xF0F0
di &= 0xF0F0
S.add(bx == di)
S.check()
m = S.model()
solved=l2b(m.eval(flag).as_long())
print(solved)
#w00TMbrR
MazinRev #
"You must take your opponent into a deep dark forest where 2+2=5".
Mikhail Tal
The challenge was made based on "Tal" mindset, escape from that forest.
难点在于函数 120b
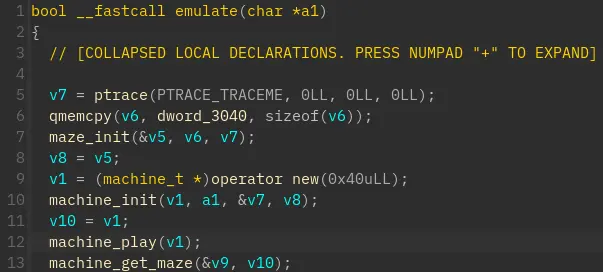
根据 sub_168e 可以推断出 v5 指向一个大小为 0x20 的结构体
根据第 9 行可以推断出 v1 是一个大小为 0x40 的结构体
易得小结构体的内容为
struct maze_t
{
int *buf;
int ptr;
int x;
int y;
int towards;
int win_or_lose;
int field_1C;
};
又易得迷宫长度为 15 宽度为 10
函数 sub_1bbc 的调用语句是错乱的
这是因为它第 4 个参数是 maze_t 结构体直接在栈上
对函数签名进行手动修正
int __usercall machine_init@<eax>(machine_t *machine@<rdi>, char *input@<rsi>, int *test@<rdx>, maze_t maze)
接下来易得大结构体的内容为
struct machine_t
{
char *insn;
maze_t maze;
int count;
int field_2C;
int *field_30;
int state;
int field_3C;
};
两个结构体做好之后 sub_1cde 的功能就不难猜了:执行用户输入求解迷宫
用户输入为 8 个字符
字符减去 65 作为指令
指令高 5 位为动作
低 3 位指示应当在哪种砖块上执行该动作,所有的动作包括(带条件的)移动、转向、旋转和将指令指针重设(即重新开始)
目标是在 8 步后到达 6 的位置
初始数据被 XOR 了 ptrace(PTRACE_TRACEME) 的结果
第一个 ptrace 是用来检测调试器的
而如果没有调试器将吸附到它的父进程
总之在第二次调用 ptrace 时一定会返回 -1
XOR -1 之后算法还将迷宫的所有 5 都转换成了 2
_ _ _ _ _ _ _ _ _ _ _ _ _ _ 6
_ _ _ _ _ _ _ _ _ _ _ _ _ _ 2
_ _ _ _ _ _ _ _ 2 3 2 2 _ 2 2
2 3 2 2 _ _ _ _ 2 _ _ 2 2 2 _
2 _ _ 2 2 2 _ _ 3 _ _ _ _ 4 _
3 _ _ _ _ 3 _ _ 2 2 4 _ _ _ _
2 2 4 _ _ 2 _ _ _ 2 _ _ _ _ _
_ 2 _ _ 4 2 2 _ 2 2 _ _ _ _ _
_ 2 _ _ _ _ 2 2 2 _ _ _ _ _ _
_ _ _ _ _ _ _ _ 4 _ _ _ _ _ _
观察发现路径是由一大堆 L 字形组合而成的
当 L 的终端为砖块 4 时需要掉头
为砖块 3 时需要继续向前
为砖块 2 时需要逆时针旋转
即输入必须为 8 8 24 8 18 25 25 32,即 IIYISZZa
impossible_challenge #
I was browsing the internet and I found this binary, and for some reason, it doesn't want to give me the flag. Can you help me?
签到,XOR 69
dark_dimension #
After destroying the earth, Dormammu "the ruler of the dark dimension"
left only one magic spell that could restore the earth to its original form,
and it was hidden in a binary file, and according to the book of the Vishanti,
only Dr.Strange can find and use the spell.
Can you help Dr. Strange get the code in order to unlock the spell?
Dart 打包的程序 5.8M
基本不能直接逆向
该题的打法是时间攻击
- 由长到短输入测试字符串,如果字符串的长度恰为通关字串的长度,则程序将多停留 2 秒
- 确定长度之后,由低索引向高索引逐字节改变字串,如果当前索引处匹配上了通关字串,则程序将多停留 1 秒
#!/usr/bin/env python3
# NOTE:
# If this script keeps providing inconsistent results, consider confining it
# inside a single-core environment with docker:
# $ docker image build . -t tbased
# $ docker run -v $PWD:/app -e <opt> -it --rm --cpus='1' tbased <prog>
import string
import subprocess
import timeit
import sys
import os
def spawn(cmd:str,_stdin:bytes)->float:
f=lambda:subprocess.Popen(cmd,stdin=subprocess.PIPE,stdout=subprocess.DEVNULL).communicate(_stdin)
return timeit.timeit(f,number=1)
def tbased(cmd:str,keys=string.digits,max_length=16,attempts=5):
print("***** TIMING BASED SIDE-CHANNEL ADVERSARY *****")
print(f"[-] Finding length of password")
sum_of_elapsed={}
for i in range(1,max_length+1):
sum_of_elapsed[i]=0.00
for _ in range(attempts):
for i in range(1,max_length+1):
sum_of_elapsed[i]+=spawn(cmd,(keys[0]*i).encode())
length=max(sum_of_elapsed,key=sum_of_elapsed.get)
print(f"[+] Done! Assuming password length to be {length}")
print(f"[-] Finding password")
p=""
for j in range(length):
sum_of_elapsed = {}
for k in keys:
payload=p+k+keys[0]*(length-1-len(p))
sum_of_elapsed[k]=spawn(cmd,payload.encode())
c=max(sum_of_elapsed,key=sum_of_elapsed.get)
p+=c
print(f"[+] Done: Assuming p[{j}] to be {c}")
if len(p)==0:
print("[-] Attack failed.")
return None
print(f"[+] Done! Password is \n{p}")
return p
if __name__=="__main__":
if len(sys.argv)<2:
print("Usage: docker run -v $PWD:/app -e <opt> -it --rm --cpus='1' tbased <prog>")
exit(0)
cmd=f"/app/{sys.argv[1]}"
keys=os.environ["TBASED_CHARSET"] if "TBASED_CHARSET" in os.environ else string.digits
max_length=os.environ["TBASED_MAX_LEN"] if "TBASED_MAX_LEN" in os.environ else 16
attempts=os.environ["TBASED_ATTEMPTS"] if "TBASED_ATTEMPTS" in os.environ else 5
result=tbased(cmd=cmd,keys=keys,max_length=max_length,attempts=attempts)
if result is not None:
print("***** EXECUTION *****")
subprocess.Popen(cmd,stdin=subprocess.PIPE).communicate(result.encode())
FROM python:slim
LABEL Maintainer="ctf"
VOLUME /app
COPY tbased.py /
RUN chmod a+x /tbased.py
ENTRYPOINT ["/tbased.py"]
docker image build . -t tbased
尽管 Python 本身是占单核的,有时候子程序可能会利用多个核导致时间不准确
解决办法是在 Docker 中运行时间攻击并设置 CPU 数量为 1
docker run -v $PWD:/app -it --rm --cpus="1" tbased dark_dimension
可以见得该程序的比较方式是逐字符比较
The Messager #
A spy was recently caught, he was leaking important data. We could recover the data leaked as well as his machine.
明文空间只有单个字符,又有 RSA 的公钥可以随意加密
因此可以 CPA,对所有字符打表
The Matrix #
After reading some papers about the DLP, I thought that working with matrices
will improve the hardness of the DLP so I made my own cryptosystem.
Author : haithem_lamri
$D^{\alpha} = P$ 求解 $\alpha$
把 $D$ 对角化得到 [37, 31, 29, 23, 19, 17, 13, 11, 7, 5, 3, 2]
可以把矩阵的离散对数问题转化为正常的离散对数问题
再用 sage 求解离散对数即可
import json
from Crypto.Hash import SHA256
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from sage.all import *
p = 12143520799543738643
def read_matrix(file_name):
data = open(file_name, 'r').read().strip()
rows = [list(eval(row)) for row in data.splitlines()]
return Matrix(GF(p), rows)
D = read_matrix('matrix.txt')
P = read_matrix('public_key.txt')
digD ,A = D.diagonalization()
digP = A.inverse() * P * A
vD = [digD[i][i] for i in range(12)]
vP = [digP[i][i] for i in range(12)]
G = GF(p)
K = discrete_log(G(vP[11]), G(vD[11]))
key = SHA256.new(data=str(K).encode()).digest()
with open("encrypted_flag.txt", "r") as ff:
data_dict = json.load(ff)
iv = bytes.fromhex(data_dict["iv"])
ciphertext = bytes.fromhex(data_dict["ciphertext"])
cipher = AES.new(key, AES.MODE_CBC, iv)
flag = cipher.decrypt(ciphertext).decode()[:46]
print(flag)
#CyberErudites{Di4g0n4l1zabl3_M4tric3s_d4_b3st}
Franklin-last-words #
Franklin gave birth to the amazing show blacklist but before he leaves the stage
he left us some few words as well as a certain machine that generates encrypted messages
$R$ 是 64 比特随机数
$c = (R+m^3)^e \pmod N$
已知 $e = 3$, $R^e$, $c$
根据公式 $(R+m^3)^3 = R^3 + 3m^3R^2 + 3m^6R + m^9$
如果知道 $m_1$ 和 $m_2$ 的密文就可以构造出 $m_3$ 的密文,当然,要先算出 $\lambda_1$ 和 $\lambda_2$
$$ \begin{bmatrix} 3m_1^3 & 3m_2^3 \newline 3m_1^6 & 3m_2^6 \end{bmatrix} \cdot \begin{bmatrix} \lambda_1 \newline \lambda_2 \end{bmatrix} = \begin{bmatrix} 3m_3^3 \newline 3m_3^6 \end{bmatrix} $$
令 $m_1 = 67$, $m_2 = 121$ (字母 C 和 y)
可以求出左边矩阵的逆
然后遍历 $m_3$ 打表即可
from sage.all import *
with open("message.py", "r") as f:
exec(f.read())
R_3 = ct[0]
def vec(pt):
return [(3*pow(pt, 3, N)) % N, (3*pow(pt, 6, N)) % N]
def ct2val(val, pt):
return (val - R_3 - pow(pt, 9, N)) % N
def val2ct(vec, num):
return (vec + R_3 + pow(pt, 9, N)) % N
prefix = b"CyberErudites{}"
vec1 = vec(prefix[0])
vec2 = vec(prefix[1])
T = matrix(Zmod(N), [[vec1[0],vec2[0]], [vec1[1],vec2[1]]])
T_ = T.inverse()
val1 = ct2val(ct[1], prefix[0])
val2 = ct2val(ct[2], prefix[1])
table = {}
for pt in range(32, 127):
mat = vector(vec(pt))
l1,l2 = T_ * mat
val3 = (val1*l1 + val2*l2) % N
table[val2ct(val3, pt)] = chr(pt)
flag = "".join([table[v] for v in ct[1:]])
print(flag)
#CyberErudites{Fr4nkl1n_W3_n33d_an0th3R_S3450N_A54P}