XCTF-ACTF2025
deeptx #
I’m fantasizing again, fantasizing about getting into Zhejiang University, successfully graduating, starting my own business, and establishing DeepSeek.
tip: sha256 of flag is fe6c63ce926ab3ed8aba9f52a3a3b8b5ef34d00c89708fba719c4cd13d0a9d73
P.S. Postcards will be sent as gifts to randomly selected teams who solve this problem.
hint: https://en.wikipedia.org/wiki/Motion_blur_(media)
从 IDA 中可以看到该题使用了 CUDA 处理图片的内容
其中图片的长度为 0x10000 也就是 256x256
CUDA 的设置为 256 线程块,每个线程块 256 个线程(仅 x 维度)
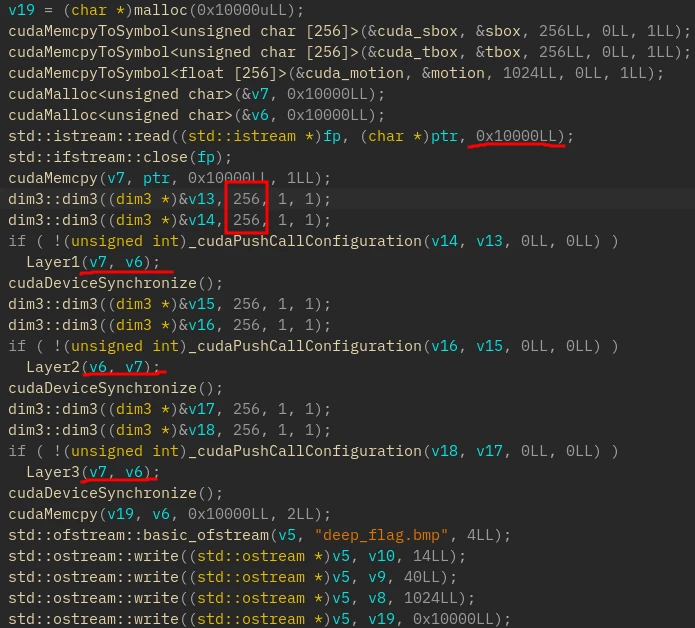
总共有三层处理函数,使用 cuobjdump 将 PTX 汇编导出(汇编和 C 伪代码框架来自 @Ning)
阅读汇编并翻译成 C 伪代码
根据已知的 CUDA 设置,在下面的伪代码中,ctaid.x 和 tid.x 将遍历 0~255,而 ntid.x 为 256 因为一个线程块里有 256 个线程(x 维度)
#include <math.h>
#include <stdint.h>
extern float cuda_motion[256];
extern uint8_t cuda_sbox[256];
extern uint8_t cuda_tbox[256];
extern void cuda_sync_thread();
void layer1(unsigned char *input, unsigned char *output, uint32_t ctaid_x,
uint32_t tid_x) {
float sum = 0.0f;
if (tid_x < 241 && ctaid_x < 241) {
for (uint32_t i = 0; i < 16; i++) {
uint32_t motion_offset = 16 * (15 - i);
uint32_t pos = (i + ctaid_x) * 256 + tid_x;
for (uint32_t j = 0; j < 16; j++) {
uint8_t in_val = input[pos];
float motion_val = cuda_motion[motion_offset + j]; // motion[15-i][j]
sum += motion_val *
(float)in_val; // sum += motion[15-i][j]*input[y+i][x+j]
// 动态模糊算法
pos++;
}
}
}
uint32_t out_idx = ctaid_x * 256 + tid_x;
output[out_idx] = (uint8_t)floor(sum);
}
void layer2(unsigned char *input, unsigned char *output, uint32_t ctaid_x,
uint32_t tid_x) {
uint32_t in_idx = ctaid_x * 256 + tid_x;
uint8_t sbox_tid = cuda_sbox[tid_x];
uint8_t sbox_ctaid = cuda_sbox[ctaid_x];
uint32_t out_idx = 256 * sbox_tid + sbox_ctaid;
output[out_idx] = input[in_idx]; // 基于 s 盒的置换,要注意 256 乘在哪?
}
void layer3(unsigned char *input, unsigned char *output, uint32_t ctaid_x,
uint32_t tid_x) {
uint32_t idx = ctaid_x * 256 + tid_x;
// 阶段 1: XOR
uint16_t tid_x_16 = (uint16_t)tid_x;
uint16_t ctaid_x_16 = (uint16_t)ctaid_x;
input[idx] ^= ctaid_x_16 | tid_x_16;
cuda_sync_thread(); // 是的这很重要,要等所有线程在它们的单元上都做完 XOR 才继续加密!
// 阶段 2: Feistel 网络
uint32_t left, right;
if ((tid_x & 7) == 0) {
left = *(uint32_t *)&input[idx];
right = *(uint32_t *)&input[idx + 4];
uint32_t key = 1786956040;
for (uint32_t i = 0; i < 3238567; i++) {
uint32_t f = ((left << 4) + 1386807340) ^ ((left >> 5) + 2007053320) ^
(left + key);
right = right + f;
f = ((right << 4) + 621668851) ^ ((right >> 5) - 862448841) ^
(right + key);
left = left - f;
key += -1708609273;
}
*(uint32_t *)&input[idx] = left;
*(uint32_t *)&input[idx + 4] = right;
}
cuda_sync_thread();
// 阶段 3: 再次 XOR
input[idx] ^= ctaid_x_16 & tid_x_16;
cuda_sync_thread();
// 阶段 4: S-Box 和 T-Box
// 这个阶段其实是矩阵相乘
// 会得到一个 sums 矩阵 (16 位)
// 想要逆向直接乘上一个逆矩阵即可
uint16_t sbox_val = cuda_sbox[tid_x];
uint16_t sum = 0;
uint32_t k = ctaid_x * 256;
for (uint32_t i = 0; i < 256; i++) {
uint8_t in_val = input[k];
uint8_t tbox_val = cuda_tbox[sbox_val & 0xFF];
sum += (uint16_t)tbox_val * in_val;
sbox_val = sbox_val * 5 + 17;
k++;
}
// 阶段 5: 最终循环
// 其实 sums 矩阵的 16 位完全没有意义
// 因为最后的 buffer 矩阵只有 8 位也就是模 256 的,只要取 8
// 位倒着算一遍即可 也不用爆破
uint32_t xor_val = ctaid_x ^ tid_x;
for (uint32_t i = 8; i < 4137823; i++) {
uint16_t temp = (sum << 3) | ((sum & 224) >> 5);
uint32_t idx = (temp * 13 + xor_val) & 0xFFFF;
uint8_t tbox_val = cuda_tbox[i & 255];
sum = cuda_sbox[(tbox_val ^ idx) & 0xFF];
}
output[idx] = (uint8_t)sum;
}
layer 3 的前三个阶段都是平凡的,第四个阶段本质上是和一个常量矩阵右乘,只要在得到 sum 组成的矩阵之后,右乘那个矩阵模 256 意义下的逆矩阵即可
而第五个阶段中无需在乎 sum 的位数,因为最终求解出的矩阵内容均为 8 位,sum 只要保留 8 位结果都是一样的(模 256),倒过来计算 sum 即可
唯一的问题是,Feistel 阶段的轮数和第五个阶段的轮数过于巨大,必须借助 CUDA 加速,将任务分块为 256x256 个单元来跑
第五个阶段的解密代码:(框架来自 @Ning,算力由 @heshi 提供)
import numpy as np
from numba import cuda
import struct
import os
import pickle
from sage.all import Zmod, Matrix
cuda_sbox = np.array([0xD6, 0x90, 0xE9, 0xFE, 0xCC, 0xE1, 0x3D, 0xB7, 0x16, 0xB6, 0x14, 0xC2, 0x28, 0xFB, 0x2C, 0x05, 0x2B, 0x67,
0x9A, 0x76, 0x2A, 0xBE, 0x04, 0xC3, 0xAA, 0x44, 0x13, 0x26, 0x49, 0x86, 0x06, 0x99, 0x9C, 0x42, 0x50, 0xF4,
0x91, 0xEF, 0x98, 0x7A, 0x33, 0x54, 0x0B, 0x43, 0xED, 0xCF, 0xAC, 0x62, 0xE4, 0xB3, 0x1C, 0xA9, 0xC9, 0x08,
0xE8, 0x95, 0x80, 0xDF, 0x94, 0xFA, 0x75, 0x8F, 0x3F, 0xA6, 0x47, 0x07, 0xA7, 0xFC, 0xF3, 0x73, 0x17, 0xBA,
0x83, 0x59, 0x3C, 0x19, 0xE6, 0x85, 0x4F, 0xA8, 0x68, 0x6B, 0x81, 0xB2, 0x71, 0x64, 0xDA, 0x8B, 0xF8, 0xEB,
0x0F, 0x4B, 0x70, 0x56, 0x9D, 0x35, 0x1E, 0x24, 0x0E, 0x5E, 0x63, 0x58, 0xD1, 0xA2, 0x25, 0x22, 0x7C, 0x3B,
0x01, 0x21, 0x78, 0x87, 0xD4, 0x00, 0x46, 0x57, 0x9F, 0xD3, 0x27, 0x52, 0x4C, 0x36, 0x02, 0xE7, 0xA0, 0xC4,
0xC8, 0x9E, 0xEA, 0xBF, 0x8A, 0xD2, 0x40, 0xC7, 0x38, 0xB5, 0xA3, 0xF7, 0xF2, 0xCE, 0xF9, 0x61, 0x15, 0xA1,
0xE0, 0xAE, 0x5D, 0xA4, 0x9B, 0x34, 0x1A, 0x55, 0xAD, 0x93, 0x32, 0x30, 0xF5, 0x8C, 0xB1, 0xE3, 0x1D, 0xF6,
0xE2, 0x2E, 0x82, 0x66, 0xCA, 0x60, 0xC0, 0x29, 0x23, 0xAB, 0x0D, 0x53, 0x4E, 0x6F, 0xD5, 0xDB, 0x37, 0x45,
0xDE, 0xFD, 0x8E, 0x2F, 0x03, 0xFF, 0x6A, 0x72, 0x6D, 0x6C, 0x5B, 0x51, 0x8D, 0x1B, 0xAF, 0x92, 0xBB, 0xDD,
0xBC, 0x7F, 0x11, 0xD9, 0x5C, 0x41, 0x1F, 0x10, 0x5A, 0xD8, 0x0A, 0xC1, 0x31, 0x88, 0xA5, 0xCD, 0x7B, 0xBD,
0x2D, 0x74, 0xD0, 0x12, 0xB8, 0xE5, 0xB4, 0xB0, 0x89, 0x69, 0x97, 0x4A, 0x0C, 0x96, 0x77, 0x7E, 0x65, 0xB9,
0xF1, 0x09, 0xC5, 0x6E, 0xC6, 0x84, 0x18, 0xF0, 0x7D, 0xEC, 0x3A, 0xDC, 0x4D, 0x20, 0x79, 0xEE, 0x5F, 0x3E,
0xD7, 0xCB, 0x39, 0x48], dtype=np.uint8)
cuda_tbox = np.array([0x62, 0x7C, 0x76, 0x7A, 0xF2, 0x6A, 0x6E, 0xC4, 0x30, 0x00, 0x66, 0x2A, 0xFE, 0xD6, 0xAA, 0x76, 0xCA, 0x82,
0xC8, 0x7C, 0xFA, 0x58, 0x46, 0xF0, 0xAC, 0xD4, 0xA2, 0xAE, 0x9C, 0xA4, 0x72, 0xC0, 0xB6, 0xFC, 0x92, 0x26,
0x36, 0x3E, 0xF6, 0xCC, 0x34, 0xA4, 0xE4, 0xF0, 0x70, 0xD8, 0x30, 0x14, 0x04, 0xC6, 0x22, 0xC2, 0x18, 0x96,
0x04, 0x9A, 0x06, 0x12, 0x80, 0xE2, 0xEA, 0x26, 0xB2, 0x74, 0x08, 0x82, 0x2C, 0x1A, 0x1A, 0x6E, 0x5A, 0xA0,
0x52, 0x3A, 0xD6, 0xB2, 0x28, 0xE2, 0x2E, 0x84, 0x52, 0xD0, 0x00, 0xEC, 0x20, 0xFC, 0xB0, 0x5A, 0x6A, 0xCA,
0xBE, 0x38, 0x4A, 0x4C, 0x58, 0xCE, 0xD0, 0xEE, 0xAA, 0xFA, 0x42, 0x4C, 0x32, 0x84, 0x44, 0xF8, 0x02, 0x7E,
0x50, 0x3C, 0x9E, 0xA8, 0x50, 0xA2, 0x40, 0x8E, 0x92, 0x9C, 0x38, 0xF4, 0xBC, 0xB6, 0xDA, 0x20, 0x10, 0xFE,
0xF2, 0xD2, 0xCC, 0x0C, 0x12, 0xEC, 0x5E, 0x96, 0x44, 0x16, 0xC4, 0xA6, 0x7E, 0x3C, 0x64, 0x5C, 0x18, 0x72,
0x60, 0x80, 0x4E, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEF, 0xB8, 0x14, 0xDE, 0x5E, 0x0A, 0xDA, 0xE0, 0x32,
0x3A, 0x0A, 0x48, 0x06, 0x24, 0x5C, 0xC2, 0xD2, 0xAC, 0x62, 0x90, 0x94, 0xE4, 0x78, 0xE6, 0xC8, 0x36, 0x6C,
0x8C, 0xD4, 0x4E, 0xA8, 0x6C, 0x56, 0xF4, 0xEA, 0x64, 0x7A, 0xAE, 0x08, 0xBA, 0x78, 0x24, 0x2E, 0x1C, 0xA6,
0xB4, 0xC6, 0xE8, 0xDC, 0x74, 0x1E, 0x4A, 0xBC, 0x8A, 0x8A, 0x70, 0x3E, 0xB4, 0x66, 0x48, 0x02, 0xF6, 0x0E,
0x60, 0x34, 0x56, 0xB8, 0x86, 0xC0, 0x1C, 0x9E, 0xE0, 0xF8, 0x98, 0x10, 0x68, 0xD8, 0x8E, 0x94, 0x9A, 0x1E,
0x86, 0xE8, 0xCE, 0x54, 0x28, 0xDE, 0x8C, 0xA0, 0x88, 0x0C, 0xBE, 0xE6, 0x42, 0x68, 0x40, 0x98, 0x2C, 0x0E,
0xB0, 0x54, 0xBA, 0x16], dtype=np.uint8)
#cuda_inv_sbox=[cuda_sbox.index(i) for i in range(256)]
#print(f"{cuda_inv_sbox=}")
cuda_inv_sbox=np.array(
[113, 108, 122, 184, 22, 15, 30, 65, 53,
235, 208, 42, 228, 172, 98, 90, 205, 200, 219, 26, 10,
142, 8, 70, 240, 75, 150, 193, 50, 160, 96, 204, 247,
109, 105, 170, 97, 104, 27, 118, 12, 169, 20, 16, 14,
216, 163, 183, 155, 210, 154, 40, 149, 95, 121, 178, 134, 254, 244, 107, 74, 6, 251, 62,
132, 203, 33, 43, 25, 179, 114, 64, 255, 28, 227, 91,
120, 246, 174, 78, 34, 191, 119, 173, 41, 151, 93, 115, 101, 73, 206,
190, 202, 146, 99, 250, 167, 141, 47, 100, 85, 232,
165, 17, 80, 225, 186, 81, 189, 188, 237, 175, 92, 84, 187,
69, 217, 60, 19, 230, 110, 248, 39, 214, 106, 242,
231, 199, 56, 82, 164, 72, 239, 77, 29, 111, 211,
224, 130, 87, 157, 192, 182, 61, 1, 36, 195, 153,
58, 55, 229, 226, 38, 31, 18, 148, 32, 94, 127,
116, 124, 143, 103, 136, 147, 212, 63, 66, 79, 51,
24, 171, 46, 152, 145, 194, 223, 158, 83, 49, 222,
135, 9, 7, 220, 233, 71, 196, 198, 215, 21, 129, 168,
209, 11, 23, 125, 236, 238, 133, 126, 52, 166, 253,
4, 213, 139, 45, 218, 102, 131, 117, 112, 176, 0, 252,
207, 201, 86, 177, 245, 197, 180, 57, 144, 5, 162,
159, 48, 221, 76, 123, 54, 2, 128, 89, 243, 44, 249,
37, 241, 234, 138, 68, 35, 156, 161, 137, 88, 140,
59, 13, 67, 181, 3, 185], dtype=np.uint8
)
cuda_sbox_device = cuda.to_device(cuda_sbox)
cuda_tbox_device = cuda.to_device(cuda_tbox)
cuda_inv_sbox_device = cuda.to_device(cuda_inv_sbox)
# 最后一个阶段👇
# 阶段五:在mod 256 意义下倒着算一遍
@cuda.jit
def last_stage_kernel(input, output, sbox, tbox, inv_sbox):
ctaid_x = cuda.blockIdx.x
tid_x = cuda.threadIdx.x
idx = ctaid_x * 256 + tid_x
xor_val = ctaid_x ^ tid_x
sum_val = input[idx]
for i in range(4137822, 7, -1):
temp = inv_sbox[sum_val]
tbox_val = tbox[i & 255]
temp ^= tbox_val
temp = np.uint8(197*(np.uint8(temp - xor_val))) # 197*13 = 1 mod 256
sum_val = np.uint8(temp<<5)|np.uint8(temp>>3)
output[idx] = sum_val
# 这个函数包括阶段五和阶段四
def last_stage(input):
input_device = cuda.to_device(input)
output_device = cuda.device_array(256 * 256, dtype=np.uint8)
threads_per_block = 256
blocks_per_grid = 256
last_stage_kernel[blocks_per_grid, threads_per_block](
input_device,
output_device,
cuda_sbox_device,
cuda_tbox_device,
cuda_inv_sbox_device)
sums = output_device.copy_to_host()
# ...
矩阵方程求解:(CUDA 无关)
mm=[0]*256*256
for j in range(256):
sbox_val = cuda_sbox[j]
for t in range(256):
mm[t*256+j] = cuda_tbox[sbox_val]
sbox_val=(sbox_val*5+17) & 0xff # mm 是可以预先计算的,可我懒
M = Matrix(Zmod(256), 256, mm)
M_ = M**-1
S = Matrix(Zmod(256), 256, sums.tolist())
X = S*M_
result = []
for r in X.rows():
result.extend(r)
return result
费斯托,XOR,以及置换的部分:(算力由 @heshi 提供)
# layer 3 is Feistel decypher
@cuda.jit
def inv_layer3_kernel(input, output, sbox, tbox):
ctaid_x = cuda.blockIdx.x
tid_x = cuda.threadIdx.x
idx = ctaid_x * 256 + tid_x
# The Feistel part, should be okay now 👿
if (tid_x & 7) == 0:
left = np.uint32(input[idx] |
(input[idx+1] << 8) |
(input[idx+2] << 16) |
(input[idx+3] << 24)) # convert to u32
right = np.uint32(input[idx+4] |
(input[idx+5] << 8) |
(input[idx+6] << 16) |
(input[idx+7] << 24)) # convert to u32
r = 3238567
delta = np.uint32(-1708609273)
key = np.uint32(1786956040 + (r * delta)) # Reverse key schedule
for _ in range(r):
key = np.uint32(key - delta)
f = np.uint32(np.uint32(right << 4) + np.uint32(621668851)) ^\
np.uint32(np.uint32(right >> 5) + np.uint32(-862448841)) ^\
np.uint32(right + key)
left = np.uint32(left + f)
f = np.uint32(np.uint32(left << 4) + np.uint32(1386807340)) ^\
np.uint32(np.uint32(left >> 5) + np.uint32(2007053320)) ^\
np.uint32(left + key)
right = np.uint32(right - f)
output[idx] = left & 0xFF
output[idx+1] = (left >> 8) & 0xFF
output[idx+2] = (left >> 16) & 0xFF
output[idx+3] = (left >> 24) & 0xFF
output[idx+4] = right & 0xFF
output[idx+5] = (right >> 8) & 0xFF
output[idx+6] = (right >> 16) & 0xFF
output[idx+7] = (right >> 24) & 0xFF
def inv_layer3(input):
temp=np.array(input, dtype=np.uint8)
# XOR 的部分直接从 CUDA 摘出来了,反正要同步线程的,不如先做好
for i in range(256):
for j in range(256):
temp[i*256+j] ^= (i&j)
input_device = cuda.to_device(temp)
output_device = cuda.device_array(256 * 256, dtype=np.uint8)
threads_per_block = 256
blocks_per_grid = 256
inv_layer3_kernel[blocks_per_grid, threads_per_block](
input_device,
output_device,
cuda_sbox_device,
cuda_tbox_device)
output = output_device.copy_to_host()
for i in range(256):
for j in range(256):
output[i*256+j] ^= (i|j)
return output
# layer 2 is swapping
@cuda.jit
def inv_layer2_kernel(input, output, sbox, tbox):
ctaid_x = cuda.blockIdx.x
tid_x = cuda.threadIdx.x
out_idx = ctaid_x * 256 + tid_x
sbox_tid = sbox[tid_x]
sbox_ctaid = sbox[ctaid_x]
in_idx = 256 * sbox_tid + sbox_ctaid
output[out_idx] = input[in_idx]
def inv_layer2(input):
input_device = cuda.to_device(input)
output_device = cuda.device_array(256 * 256, dtype=np.uint8)
threads_per_block = 256
blocks_per_grid = 256
inv_layer2_kernel[blocks_per_grid, threads_per_block](
input_device,
output_device,
cuda_sbox_device,
cuda_tbox_device)
return output_device.copy_to_host()
只要 bmp 1078 字节后的 256x256 数据即可
with open("deep_flag.bmp", "rb") as fp:
head = fp.read(1078)
body = fp.read(0x10000)
buf = np.frombuffer(body, dtype=np.uint8)
buf = last_stage(buf)
buf = inv_layer3(buf)
buf = inv_layer2(buf)
with open("flag.bmp","wb") as fp:
fp.write(head)
fp.write(buf.tobytes())
得到 flag.bmp,不过它是动态模糊过的
虽然 cuda_motion 矩阵已知,但找一个消除动态模糊的算法并复现对一个逆向手来说还是太没有头绪了

观察到整个图片被向左下的运动拉扯模糊,通过调整 GIMP 的锐化滤镜参数,可以大致看出 flag(自右上向左下观察)

最后因为 SHA256 校验和已知,用 mbruteforce 对几个未知字符进行爆破
ACTF{DeEptCUdAR1VQUZ}
ezFPGA #
Software is too slow… and hardware is too honest.
system verilog 有几个特性需要额外关注:
assign =指的是接线,即将右边变量组成的表达式连线到左边,右边的值一旦更新左边变量也会随之更新<=指的是触发式更新,即左边的变量在所属begin块全部执行结束之后一并更新,其右边的表达式使用的变量取原来的值- .vcd 文件的输出中,如果某变量在某周期内没有显示,只能说明它在这个周期内值没有更新
加密算法可以分为两步,先看第二步:
输入为长度为 36 的字串,然后初始化一个四个状态的状态机,每个状态由重复执行数次之后就转为下一个状态,在最后一个状态输出
因此这些状态可以看作顺序执行的几个 for 循环
- S0 初始化一个 box,循环 256 次
- S1 基于一串密钥打乱这个 box,循环 256 次
- S2 由 box 生成流并加密,循环 36 次
- S3 输出加密的结果,循环 36 次
再看变量之间的接线关系
assign cd = ca + 1; // ii = ii + 1
assign ce = cb + ba[cd]; // jj = jj + box[ii]
assign cf = ba[cd] + ba[ce]; // box[ii] + box[jj]
assign ch = cg + ba[da] + db[da%8]; // j = j + box[i] + key[i%len(key)]
所以没错这其实是 RC4,密钥也给出了为 eclipsky
而 RC4 的密文只要在 .vcd 文件中找 cypher 变量出现更新的行即可
其中大概在第 9 次输出时,cypher 的值相比上个周期没有更新,因此没有输出,这个值一定要补上
再看第一步:
将输入零填充到 39 个字符
生成一个新的字串,字串下标为 i 的元素为输入的 i ~ i+4 和 (11, 4, 5, 14) 的点乘,然后再将新的字串排成 6x6 的矩阵,右乘一个已知的矩阵
将矩阵展开成字串,送入 RC4
解矩阵:(这里用了 z3 逐行求解因为一开始没反应过来是矩阵 QAQ)
expect = [(x - y) & 0xFF for x, y in zip(cipher, stream)]
ad = [
116, 174, 193, 124, 102, 100,
11, 193, 115, 4, 127, 139,
98, 214, 197, 145, 97, 151,
31, 30, 117, 15, 230, 179,
235, 25, 244, 202, 73, 222,
15, 191, 119, 140, 94, 32,
]
def stage1():
global ad
vv=[]
for i in tqdm(range(6)):
s=z3.Solver()
v=[z3.BitVec(f"v{j}",8) for j in range(6)]
for j in range(6):
s.add((
v[0]*ad[j%6]+
v[1]*ad[j%6+6]+
v[2]*ad[j%6+12]+
v[3]*ad[j%6+18]+
v[4]*ad[j%6+24]+
v[5]*ad[j%6+30]
)%256 == expect[i*6+j])
assert s.check() == z3.sat
m = s.model()
for j in range(6):
vv.append(m[v[j]])
return vv
buffer = stage1()
因为 flag 的前几个字符已知,所以可以从未知的字符开始逐字符解单变量方程,这里直接爆破了:
def stage2():
global buffer
flag=[ord('A'),ord('C'),ord('T'),ord('F')]
assert((11*flag[0]+4*flag[1]+5*flag[2]+14*flag[3])%256 == buffer[0])
charset=list(range(33,127))
charset.append(0)
for i in range(4,39):
for j in charset:
try:
if (11*flag[i-3]+4*flag[i-2]+5*flag[i-1]+14*j)%256 == buffer[i-3]:
flag.append(j)
continue
except:
print(flag)
return None
return flag
flag=stage2()
print(''.join(chr(b) for b in flag))
#ACTF{RC4_4nd_FPGA_w4lk_1nt0_4_b4r}
复盘 #
clé secrète #
C’est ma clé secrète
nc 1.95.214.243 9999
WIP
unstoppable #
OH NO I CANNOT STOP IT🤯
Thanks: https://github.com/za233/Polaris-Obfuscator
hint: https://en.wikipedia.org/wiki/Turing_machine
WIP